AC Power Analysis

Instantaneous and Average Power

          Instantaneous power is a power that absorb by a sigle element. It is also a value of power p at time t is equal to instantaneous voltage at time t times the instantaneous current at time t.

formula:

p(t) = v(t) i(t)

each  instantaneous voltage and current has its own formula:

v(t) = Vm cos(ωt + θ)

i(t) = Im cos(ωt + θ)

The Vm and the Im are the amplitudes or the peak values, and θv and θi are the phase angle of the element. 

So we arrive this formula:

                                             p(t) = v(t) i(t) = Vm Im cos (ωt + θv) cos (ωt + θi)

We apply the trigonometric identity.

cos A cos B = 1/2 [cos (A - B) + cos (A + B)]

and express Equation as:

                                  p(t) = 1/2 Vm Im cos(θv - θi) + 1/2 Vm Im cos (2ωt + θv + θi)

average power is the average power of an instantaneous power in a period.

formula given is:

                                                            P = 1/T ∫ p(t) dt

by substituting p(t) in the equation:

                        P = 1/T ∫ 1/2 Vm Im cos(θv - θi) dt  +  1/T ∫ 1/2 Vm Im cos(2ωt + θv + θi)dt

                        P = 1/2 Vm Im cos(θv - θi) 1/T ∫ dt + 1/2 Vm Im 1/T ∫ cos(2ωt + θv + θi) dt

The first integrand is constant and the average of the constant is the same. the second integrand is a sinusoid. The average of the sinusoid is over its period is 0 because the area under the sinusoid during a positive half cycle is canceled by the area under it during the following half cycle. th second tern will be vanished and the power becomes:

                                                     P = 1/2 Vm Im cos(θv - θi)

Example:

       A current I = 10∠30 A flows through an impedance Z = 20∠ -22 Ω find the average power delivered to the impedance.

First we get the voltage across the impedance Z so we can solve the power delivered to the impedance.

                                   V = IZ = (10∠30 A)(20∠ -22 Ω) = 200∠ 8 V

since we have the required voltage so:

                                     P = 1/2 Vm Im cos(θv - θi)

                                     P = 1/2 (200)(10) cos(8 - 30)

                                     P = 1000 cos(8 - 30)

                                     P = 927.18 W


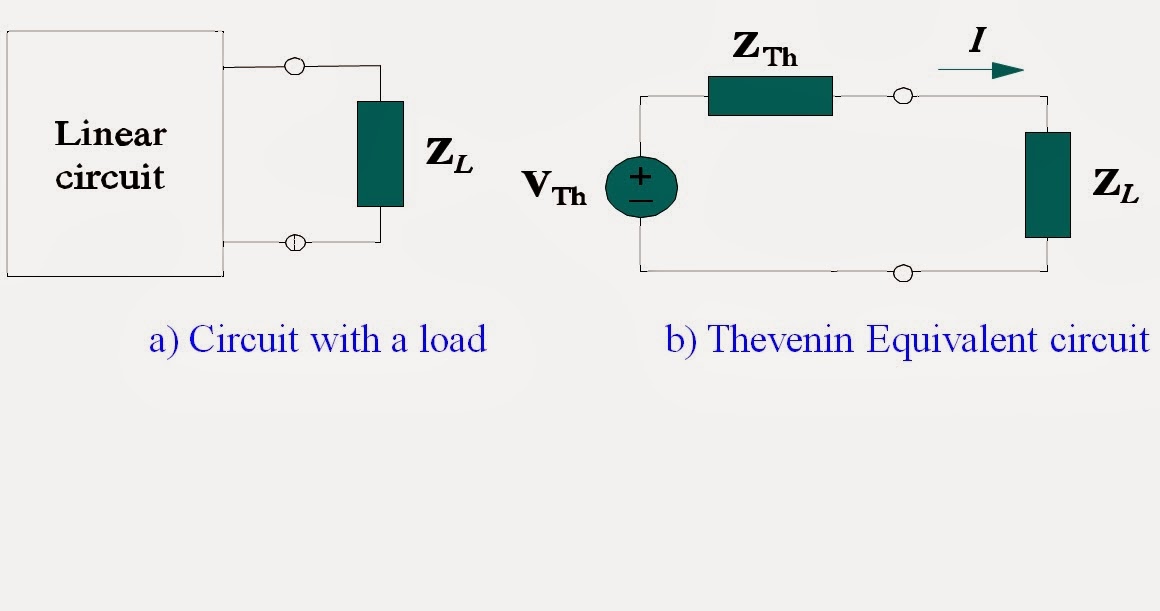
Maximum Average Power Transform

       The maximum power transfer theorem states that, to obtain maximum external power from a source with a finite internal resistance, the load impedance must equal to the complex conjugate of the thevenins impedance.

Finding the maximum average power which can be transferred from a linear circuit to a Load connected.

Load ZL represents any element that is absorbing the power generated by the circuit.

In rectangular form, the thevenin impedance ZTh and the load impedance ZL are:

Ajust RL and XL to get maximum P

Therefore: ZL = RTh - XTh = ZTh will generate the maximum power transfer.

Maximum power is:

For Maximum average power transfer to a load impedance ZL we must choose ZL as the complex conjugate of the Thevenin impedance ZTh.